Testez votre QI en maths avec les plaisirs oubliés de l'arithmétique.

Premier test : vous avez le niveau d'un Ministre de l'Education Nationale.


4 stylos valent 2,42 €, combien valent 14 stylos ?


Deuxième test : vous avez le niveau du "certif".


J'ai trois fois l'âge que vous aviez, quand j'avais l'âge que vous avez.
Quand vous aurez l'âge que j'ai, ensemble nous aurons 98 ans.
Quels sont nos âges respectifs ?


Avec la réussite à ces 2 tests, tout est possible...

Vous disposez des atouts indispensables pour être "bon" en maths.

Hercule 1, Augustine 0

Hercule : combien ça fait x/x?
Augustine : ça fait zéro;
- non, x/x, ça ne fait pas zéro;  
- si, x/x, ça fait zéro;
- et 5/5, ça fait combien?
- ça fait zéro;
- non, ça ne fait pas zéro;
- alors, ça fait combien?
- 5/5, ça ne fait pas zéro;
- ça fait zéro; si ça ne fait pas zéro, alors je sais pas;
- prends ta calculatrice et divise 5 par 5; ça fait combien?
- ha, ça fait 1;
- donc ça ne fait pas zéro;
- c'est pareil;
- tu veux dire que 1 et 0 c'est pareil.
Et ton ordinateur, il pense que 1 et  0 c'est pareil;
et "on" et "off", c'est pareil;
et 1 frère et 0 frère, c'est pareil;

et 1 en maths et 0 en maths, c'est pareil;
Augustine : presque;
Et 0/0, ça fait 1?
Hercule : diviser par zéro, mais c'est pas possible;
- ha, c'est nouveau ça !
- non, mais maintenant nous allons devoir faire travailler nos petites cellules grises;

y=1/x

voici la représentation de la fonction y=1/x
c'est une hyperbole; comme tu peux le voir Augustine, elle est en 2 parties symétriques.
Et en regardant de plus près tu comprendras que pour x=0,
il n'y a pas de valeur pour y, ni en haut, ni en bas.


Hercule :  et maintenant, si tu divises 1 par 0 avec ta calculatrice, ça fait quoi?
Augustine : ça fait "Error";


c'est mieux, mais voyons si tu peux faire ces calculs;
1/1, ça fait ..........
1/2, ça fait ..........
1/3, ça fait ..........
1/4, ça fait ..........
1/5, ça fait ..........
1/10, ça fait ..........
1/100, ça fait ..........
Et x/x, ça fait ..........., si x n'est pas ...................................

Augustine : finalement ce zéro, il n'est pas si "nul" que ça.

Denis GUEDJ : vous n'êtes pas nuls en maths

Mathisse

Henri Matisse, 1869 - 1954

Pour Henri Matisse, peindre, c'est comme résoudre une équation en trouvant la solution la plus juste et la plus élégante.

En 1952, Matisse peint La Tristesse du roi. Une belle équation résolue...

La Tristesse du roi, 1952

Avec ses précédents travaux, Matisse a découvert la richesse et la liberté de création qu'offrent ces morceaux de papiers recouverts d'une couleur unique, gouache mate faite de pigments, de chaux et de gomme arabique, et dans lesquels il découpe à vif.

C'est avec cette technique que, durant les toutes dernières années de sa vie, il va produire quelques tableaux monumentaux, oeuvres dignes des plus grandes compositions classiques.

A cet égard, La Tristesse du roi se réfère à une toile de Rembrandt, David jouant de la harpe devant Saül, où le jeune héros biblique joue pour distraire le roi de sa mélancolie, mais aussi aux autoportraits tardifs du vieux maître hollandais. Dans cette oeuvre, Matisse superpose les thèmes de la vieillesse, du regard tourné vers la vie antérieure (titre d'un poème de Baudelaire déjà illustré par l'artiste), de la musique qui apaise tous les maux.

Dans cet ultime autoportrait, le peintre se représente par cette forme noire, semblable à sa silhouette assise dans son fauteuil, entouré des plaisirs qui ont enrichi sa vie : les pétales jaunes qui s'envolent ont la gaité des notes de musique, l'odalisque verte symbolise l'Orient, tandis qu'une danseuse rend hommage au corps de la femme. Tous les thèmes matissiens sont réunis dans cette peinture magistrale.

------------------------

Rembrandt, David jouant de la harpe devant Saül

 --------------------------- 

                                                               

  La vie antérieure

J'ai longtemps habité sous de vastes portiques

Que les soleils marins teignaient de mille feux,

Et que leurs grands piliers, droits et majestueux,

Rendaient pareils, le soir, aux grottes basaltiques.

Les houles, en roulant les images des cieux,

Mêlaient d'une façon solennelle et mystique

Les tout-puissants accords de leur riche musique

Aux couleurs du couchant reflété par mes yeux.

C'est là que j'ai vécu dans les voluptés calmes, 

Au milieu de l'azur, des vagues, des splendeurs, 

Et des esclaves nus, tout imprégnés d'odeurs,

Qui me rafraîchissaient le front avec des palmes,

Et dont l'unique soin était d'approfondir

Le secret douloureux qui me faisait languir.

Charles Baudelaire

Parenthèse

Il y a, au moins deux façons de nager dans le bonheur :

- l'une est à Saint-Sauveur-Camprieu;

- et l'autre est en collant son nez sur l'un des naseaux d'un cheval, (Homeric).

SUDOKU

En maths, le meilleur résultat c'est celui que l'on trouve tout seul.

Pour vous entraîner à chercher et à trouver, à tester votre logique et votre ténacité, voici le SUDOKU.

1, 2, 3, 4, 5, 6, 7, 8, 9, à vous de jouer ...

Second brain

Hercule peut, avec ses seules petites cellules grises, résoudre cette équation du second degré
 et trouver avec un Δ > 0 les 2 racines, x' = -1 et x" = 2;

-x² + x + 2 = 0
ax² + bx + c = 0

a = -1
b = 1
c = 2

Δ = b² - 4ac
Δ = 1 -  4 (-1x2)
Δ = 9

x', x'' = -b ± √Δ / 2a

x' = -1 + √9 / -2
x' = -1 + 3 / -2
x' = -1

x" = -1 - √9 / -2
x" = -1 -3 / -2
x" = 2

Hercule peut aussi tracer la fonction y = -x² + x + 2;
il peut aussi trouver la dérivée y' et en déduire que la "parabole" passe par un Max Point
( Xm, Ym ) = ( 0,5 ; 2,25 ).

y' = -2x +1

y' = 0
-2x +1 = 0
-2x      = -1
x = 1/2 = 0,50

y = -x² +x +2
y = -(1/2)² + 1/2 +2
y = - 1/4 + 1/2 +2
y = -1/4 + 2/4 + 8/4
y = 9/4 = 2,25

Mais maintenant, Hercule a un "second brain", 2 apps :

- Math Equation Solver
- et Quick Graph

presque plus rapide...

Tout un programme : PART 1

Les 4 opérations  + - x : , avec tous les nombres

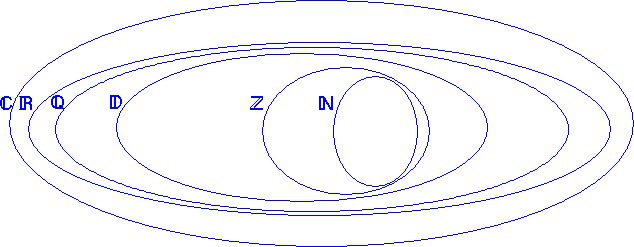
N est l'ensemble des entiers naturels :  0, 1, 2, 3 ...

Z est l'ensemble des entiers relatifs :    0, 1, 2, 3, -1, -2, -3...

D est l'ensemble des décimaux :          0, 1, 2, 3, -1, -2, -3, 2, 65 ; 5,94 ...

Q est l'ensemble des rationnels :          0, 1, 2, 3, -1, -2, -3, 2,65; 5,94; 1/2, 5/3...

R est l'ensemble des nombres réels :    0, 1, 2, 3, -1, -2, -3, 2,65 ; 5,94, 1/2, 5/3, π, √2 ...

C est l'ensemble des nombres complexes

Pour le moment et avec N, Z, D, Q, R vous devez savoir faire les 4 opérations,  + - x :

Nous allons commencer avec N et sans la moindre calculatrice :

+ ☟
55 + 28 = ..
55 + 20 + 8 = ..
55 + 20 + 5 + 3 = . .

280 + 150 = ...
280 + 100 + 50 = ...
280 + 100 + 20 + 30 = . . .

- ☟
55 - 28 = ..
55 - 20 - 8 = ..
55 - 20 - 5 - 3 = . .

280 - 150 = ...
280 - 100 - 50 = . . .

x ☟
55 x 100 = 5500
280 x 1000 = 280 000

: ☟
280 : 2 = 140 ou 140 x 2 = 280

360 : 2 = 180 ou 180 x 2 = 360
360 : 3 = 120 ou 120 x 3 = 360 ou (100 x 3) + (20 x 3) = 300 + 60 = 360

Avec Z, c'est qu'une affaire de signe + ou - :

+  ou  -  ☟
- 5 + 7 - 3 + 4 - 7 - 2 = - 5 - 3 + 4 - 2 = - . 

x  ☟
7 x - 3   = - . .
- 7 x 3   = - . .
- 7 x - 3 = + . .

:  ☟
21 : -3    = - 7  parce que - 3 x -7   = + . .
- 21 : 3   = -7  parce que 3 x -7       = - . .
- 21 : - 3 = + 7 parce que - 3 x + 7 = - . .

Avec D, c'est une histoire de virgule :

+ ou - ☟
  14 , 25
+  5 , 756
  . .  , . . .

  70 , 225
- 50 , 45 
  . .  ,  . . .

x ☟
14,25 x 10 = 142,5
5,756 x 100 = 575,6
70,225 x 1000 = . . . . .
-50,45 x 10 000 = - . . . . . .

: ☟
14,25 : 10 = 1,425
5,756 : 100 = 0,05756
70,225 : 1000 = . , . . . . . . 
- 50,45 : 10 000 = - . , . . . . . .


Encore 2 ensembles de nombres, (Q et R), et nous aurons sérieusement fait progresser nos petites
cellules grises.

Tout un programme : PART 2

                 Les 4 opérations + - x : , avec tous les nombres

Après N, Z, D poursuivons avec Q et les fractions :

+ ou - ☟
Hercule : ça fait combien 1/2 heure + 1/4 d'heure ?
Augustine : ça fait 3/4 d'heure

Hercule : donc 1/2 + 1/4 = 3/4
                 ou 2/4 + 1/4 = 3/4

On ne peut ajouter des fractions que si elles ont le même dénominateur.

1/3 + 3/4 + 2/5 = 20/60 + 45/60 + 24/60 = 89/60
avec 3 x 4 x 5 = 60

4/5 + 1/8 = . ./40 + . ./40 = . ./40
2/7 - 4/5 = - . . / . .

x ☟ 
1/2 x 1/4 = 1/8
ou  1 x 1 / 2 x 4
4/5 x 1/8 = 4 x 1 / 5 x 8 = 1 x 1 / 5 x 2 = 1/10

: ☟
1/2 : 1/4 = 1/2 x 4/1 = 4/2 = 2
4/5 : 1/8 = 4/5 x . / . = . . / .

Encore un effort avec R et les racines carrées :

Augustine : c'est quoi ça ?
Hercule : prenons un carré de 2 m de coté et calculons sa surface :
S = 2 x 2 = 4 m²
Augustine : et alors ?
Hercule : Eh bien le carré de 2, c'est la surface du carré : 2² = 4
et la racine carrée de 4, c'est le coté du carré : √4 = 2

+ ou - ☟
√2 + √3 = √2 + √3
√2 - √3 = √2 - √3

x ☟
√2 x √3 = √2 x 3 = √6
1,414 x 1,732 = 2,449

: ☟
√2  =  √2/3
√3
1,414 =  0,816
1,732

Augustine : et l'ensemble C ?
Hercule : plus tard, plus tard ;

Augustine : alors, on a fait le programme...
Hercule : ma chère Augustine, si vous savez tout faire depuis le début, vous avez accompli
d'énormes progrès et maintenant nous allons pouvoir nous amuser.

POUR CENT AGE

Voici le symbole d'un pourcentage, mais que signifie-t-il vraiment ?

Une TVA à 7%, une remise de 25%, un livret A à 2,25%...





TVA de 7% :
pour un prix HT de 100€,  la TVA est de 7€,  le prix TTC est de 107€
ou
pour un prix HT de 1€,  la TVA est de 0,07€,  le prix TTC est de 1,07€

Remise de 25% :
pour un prix TTC de 100€, la remise est de 25€, le prix TTC à payer est de 75€
ou
pour un prix TTC de 1€, la remise est de 0,25€, le prix TTC à payer est de 0,75€

livret A à 2,25% :
pour 100€ placés pendant un an, les intérêts sont de 2,25€, le capital obtenu est de 102,25€
ou
pour 1€ placé pendant un an, l'intérêt est de 0,0225€, le capital obtenu est de 1,0225€


Un pour cent age, (pourcentage), signifie pour 100 ...
Un pourcentage, c'est aussi une fraction ou un nombre décimal :

7% = 7/100 = 0,07
25% = 25/100 = 1/4 = 0,25
2,25% = 225/10 000 = 9/400 = 0,0225

A présent et sans calculatrice, faisons travailler nos petites cellules grises :

Une TVA de 7% :
pour un prix HT de 500€,  la TVA est de . . €,  le prix TTC est de . . . €
pour un prix HT de 1000€,  la TVA est de . . €, le prix TTC est de . . . . €

Une remise de 25% :
pour un prix TTC de 800€,  la remise est de . . . €, le prix TTC est de . . . €
pour un prix TTC de 2000€,  la remise est de . . . €, le prix TTC est de . . . . €

le livret A à 2,25% :
pour 1 000€ placés pendant un an,  les intérêts sont de . . , . . €,  le capital obtenu est de . . . . , . . €
pour 10 000€ placés pendant un an, les intérêts sont de . . . €,  le capital obtenu est de . .  . . . €


Trop facile. A présent il nous faut trouver directement le prix TTC ou le prix HT

TVA 7% :
                      prix HT = 19€                prix TTC = 20,33€                      



A vous de trouver le programme le plus simple, (une opération), pour avoir directement le résultat,
bien entendu, après avoir choisi le taux de TVA.


A vous de trouver directement le prix à payer pour un article à 19€, avec une remise de 25% :

Remise 25% :

                    prix TTC = 19€             prix à payer = . . , . . €

A vous de trouver directement le capital obtenu avec 19 000€ placés pendant un an à 2,25% :

livret A à 2,25% :

          capital placé = 19 000€            capital obtenu = . .  . . . , . . €

APPRENDRE

Il n'est plus aisé pour apprendre que d'apprendre à autrui.

Par exemple : apprenez-moi l'addition...

59 + 17 = 
50 + 9 + 10 + 7 = 
50 + 10 + 9 + 7 = 
50 + 10 + 16 =
50 + 10 + 10 + 6 =
70 + 6 = ..

     1      
     59
  + 17
    _____
     . .

Avez-vous déjà essayé de faire une mayonnaise sans oeufs ?

Difficile, voire impossible.

Et sans outils, (cuillère, fouet) ?

Alors là, impossible...

C'est la même chose avec les maths.

Il faut un minimum d'outils pour faire des maths, mais aussi pour toutes sortes de travaux professionnels ou autres activités quotidiennes.

Par exemple, il faut connaître les 4 opérations, avec les nombres entiers, mais aussi avec les autres nombres... 


Sans la maîtrise de ces outils, c'est comme si l'on voulait faire une mayonnaise sans oeufs.

La tâche du philosophe ou LOU SALOMÉ & FRIEDRICH NIETZSCHE in ONFRAY - LEROY : NIETZSCHE Se créer liberté

LOU SALOMÉ :
Et votre tâche...
Vous voudrez bien m'en dire plus ?

FRIEDRICH NIETZSCHE :
Bien sûr, avec plaisir.
Mais comment vous dire tout ça en peu de mots...
Et par quoi commencer ?

LS :
Par le commencement !

FN :
Le commencement c'est la fin...

LS :
Ah oui...

FN :
Le commencement, c'est la fin, parce qu'au début, on trouve l'éternel retour qui, en fait, est aussi au milieu et à la fin...

LS :
Autrement dit ?

FN :
Tout est fatalité, nécessité, on ne choisit rien.

La volonté de puissance, voilà la force qui meut toute réalité !

Plus besoin de DIEU.
Il n'y a plus qu'éternel retour des choses et volonté de puissance.

LS :
C'est effrayant ce que vous annoncez, effrayant...

FN :
Oui, le mot n'est pas trop fort, mais réjouissant en même temps.
Voilà qui permet à nouveau une philosophie tragique.

LS :
Et pourquoi réjouissant ?
Parce que tout de même, au vu de ce que vous dites...

FN :
Réjouissant parce que cette vérité tragique libère.

LS :
De quoi ?

FN :
De nous ! Du fardeau d'avoir à être...

LS :
Et de quelle manière ?

FN :
L'éternel retour est un principe sélectif. Devant chaque moment de l'existence où nous hésitons, il nous faut dire...
"Choisissons ce qui devra se répéter sans cesse",
"Préférons ce qui reviendra éternellement"...

Et là, tout devient simple !

Il faut aimer ce qui advient, "Amor fati", "Aime ton destin".

C'est d'ailleurs la formule du bonheur...

Du moins la conjuration du malheur, c'est la plus haute sagesse.

LS :
Et votre tâche dans tout ça ?

FN :
Justement, révéler tout ça, le dire, le raconter, l'expliquer, c'est la tâche du philosophe.

Enseigner la nature tragique du monde, puis donner des solutions pour y vivre et parvenir à la joie.

MATHOU